数据结构
在2025年的4月12日是一个周六我参加了我人生中的第一次比赛,是蓝桥杯的c++的程序设计。在参加前自己对数据结构的学习只是囫囵吞枣,并没有真正的去融会贯通,所以接下来这个系列我会将数据结构的内容重新复盘一遍并且加深理解与学习!
可能会用到的单词
数据结构肯定少不了要记单词
对数据结构的操作(记忆思路 )- > 创销,增删改查。
数据
数据结构的三要素
逻辑结构
定义一种数据结构
集合结构
线性结构
一对一
树状结构
一对多
图状结构
多对多
数据的运算
针对于某种逻辑结构,结合实际需求,定义基本运算。
物理结构(存储结构)
如何用计算机实现这种数据结构
非顺序储存
顺序存储
链式存储
索引存储
散列存储
算法
什么是算法
程序 = 数据结构 + 算法
算法(Algorithm)是对特定问题求解步骤的一种描述,它是指令的有限序列,其中的每条指令表示一个或多个操作。
算法的特性
有穷性
确定性
算法中每条指令必须有确定的含义,对于相同的输入只能得出相同的输出。
可行性
算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
输入
一个算法有零个或多个输入,这些输入取自于某个特定的对象的集合。
输出
一个算法有一个或多个输出,这些输出是与输入有着某种特定关系的量。
"好"算法的特质
正确性
算法应该能购正确的解决求解问题。
可读性
算法应具有良好的可读性,以帮助人们理解。
健壮性
输入非法数据时,算法能适当地作出反应或者进行处理,而不会产生莫名其妙的输出。
高效率与低存储量需求
算法执行省时 时间复杂度低、省内存 空间复杂度低。
🍅复杂度分析
⛓数组与链表
顺序表
顺序表的优点与局限性
数组存储在连续的内存空间内,且元素类型相同。这种做法包含丰富的先验信息,系统可以利用这些信息来优化数据结构的操作效率。
空间效率高:数组为数据分配了连续的内存块,无须额外的结构开销。
支持随机访问:数组允许在 O(1) 时间内访问任何元素。
缓存局部性:当访问数组元素时,计算机不仅会加载它,还会缓存其周围的其他数据,从而借助高速缓存来提升后续操作的执行速度。
连续空间存储是一把双刃剑,其存在以下局限性。
插入与删除效率低:当数组中元素较多时,插入与删除操作需要移动大量的元素。
长度不可变:数组在初始化后长度就固定了,扩容数组需要将所有数据复制到新数组,开销很大。
空间浪费:如果数组分配的大小超过实际所需,那么多余的空间就被浪费了。
顺序表的典型应用
数组是一种基础且常见的数据结构,既频繁应用在各类算法之中,也可用于实现各种复杂数据结构。
随机访问:如果我们想随机抽取一些样本,那么可以用数组存储,并生成一个随机序列,根据索引实现随机抽样。
排序和搜索:数组是排序和搜索算法最常用的数据结构。快速排序、归并排序、二分查找等都主要在数组上进行。
查找表:当需要快速查找一个元素或其对应关系时,可以使用数组作为查找表。假如我们想实现字符到 ASCII 码的映射,则可以将字符的 ASCII 码值作为索引,对应的元素存放在数组中的对应位置。
机器学习:神经网络中大量使用了向量、矩阵、张量之间的线性代数运算,这些数据都是以数组的形式构建的。数组是神经网络编程中最常使用的数据结构。
数据结构实现:数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如,图的邻接矩阵表示实际上是一个二维数组。
树
叉树常见术语
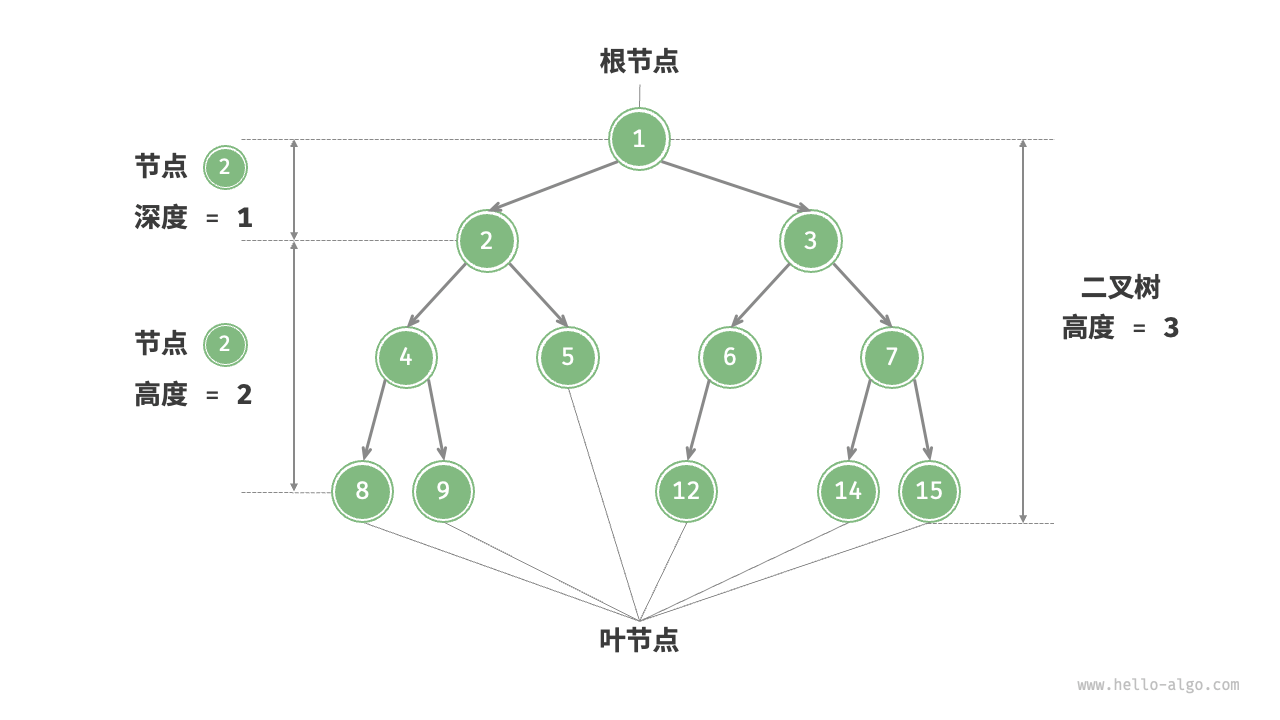
二叉树的常用术语如图 7-2 所示。
根节点(root node):位于二叉树顶层的节点,没有父节点。
叶节点(leaf node):没有子节点的节点,其两个指针均指向 None 。
边(edge):连接两个节点的线段,即节点引用(指针)。
节点所在的层(level):从顶至底递增,根节点所在层为 1 。
节点的度(degree):节点的子节点的数量。在二叉树中,度的取值范围是 0、1、2 。
二叉树的高度(height):从根节点到最远叶节点所经过的边的数量。
节点的深度(depth):从根节点到该节点所经过的边的数量。
节点的高度(height):从距离该节点最远的叶节点到该节点所经过的边的数量。
Tip
请注意,我们通常将“高度”和“深度”定义为“经过的边的数量”,但有些题目或教材可能会将其定义为“经过的节点的数量”。在这种情况下,高度和深度都需要加 1 。
树的类型
树的遍历
主要常用的遍历方法有前序遍历,中序遍历,后序遍历和层序遍历。但是多叉树的遍历没有中序遍历。
